Дистанційна освіта з інформатики за травень 2021 року
в період
11.05.2021-16.09.2021
Теоретична частина
Створення та аналіз математичної моделі лінійних рівнянь з параметром для "коректного" опрацювання в алгоритмі пошуку унікальних коренів за відомими властивостями.
Запитання 1. Як аналізувати математичні моделі лінійних рівнянь з параметрами, якщо корені рівняння мають бути тільки від’ємними числами?
Відповідь. Продемонструємо зразок аналізу такого лінійного рівняння з параметром.
Завдання 1. Знайти такі значеннях параметра а, при яких рівняння
-4х + 5а +8= -3а+2ах-10
з невідомим х має тільки від’ємні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Аналіз математичної моделі.
-4х + 5а +8= -3а+2ах-10
-4х -2ах+ 5а +8= -3а-10
-4х -2ах = -3а-10-5а-8
-2(2+а)х = -8а-18
-2(2+а)х = -2(4а+9)
(2+а)х = (4а+9)
Якщо 2+а=0, тобто а =-2, тоді 4*(-2)+9=1. Отримаємо: 0х=1.
Якщо а= -2, то дане рівняння немає коренів.
(2+а)х = (4а+9)
х = (4а+9)/(2+а). Знайдемо нулі чисельника і нулі знаменника. Це такі числа: а= -2.25; а= -2.
Відповідно умові задачі, має виконувати нерівність: (4а+9)/(2+а)<0, тобто корені рівняння мають бути від’ємними числами. Розглянемо два випадки: а)чисельник - це додатне число, знаменник - це від’ємне число; б) чисельник - це від’ємне число, знаменник - це додатне число;
Випадок 1. Система двох нерівностей: 4а+9<0 i 2+а>0, система немає розв’язків.
Випадок 2. Система двох нерівностей: 4а+9>0 i 2+а<0, розв’язки системи: ає(-2.25; -2)
aбо -2.25<a<-2.
Відповідь: Якщо параметр -2.25 <a< -2, то рівняння
-4х + 5а +8= -3а+2ах-10
з невідомим х має тільки від’ємний корінь х = (4а+9)/(2+а).
Реалізація мовою програмування Python3.
print('Якщо множина параметрa -2.25 <a< -2, то рівняння')
print('то корінь х = (4а+9)/(2+а) для даного рівняння')
print('-4х + 5а +8= -3а+2ах-10 знаходяться на інтервалах: -оо <х<0.')
k=300; a1=-2.25; a2=-2; h=(a2-a1)/k; a=['None']*k;
for j in range(3,k):
a[j]=float(-2.25+float(h*j))
z=float((4*a[j]+9))
u=float(2+a[j])
x=float(z/u)
print(j,'-ий випадок. Якщо параметр a=',a[j],' то корінь рівняння x(a)=',x)
Протестувати програму декілька разів.
Тест 1. Якщо k=5.
Тест 2. Якщо k=10.
Тест 3. Якщо k=100.
Запитання 2. Як аналізувати математичні моделі лінійних рівнянь з параметрами, якщо корені рівняння мають бути тільки додатними числами?
Відповідь. Продемонструємо зразок аналізу такого лінійного рівняння з параметром.
Завдання 2. Знайти усі такі значеннях параметра а, при яких рівняння
-3ах + 4а = -2а+4х-4
з невідомим х має тільки додатні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Аналіз математичної моделі.
-3ах + 4а = -2а+4х-4
-3ах-4х= - 4а -2а+-4
-(3а+4)х=-(6а+4)
(3а+4)х=(6а+4)
х=(6а+4)/(3a+4), якщо а< >-4/3
Якщо а=-4/3, тоді 6*(-4/3)+4=-4. Отримаємо: 0х=-4.
Якщо а= -4/3, то дане рівняння немає коренів.
(4+3а)х = (4+6a)
х = (6а+4)/(4+3а). Знайдемо нулі чисельника і нулі знаменника. Це такі числа: а= -4/3; а= -2/3.
Відповідно умові задачі, має виконувати нерівність: (6а+4)/(4+3а)>0, тобто корені рівняння мають бути додатними числами. Розглянемо два випадки: а)чисельник - це додатне число, знаменник - це додатне число; б) чисельник - це від’ємне число, знаменник - це від’ємне число;
Випадок 1. Система двох нерівностей: 6а+4>0 i 4+3а>0, система має розв’язки ає( -2/3; +oo) .
Випадок 2. Система двох нерівностей: 6а+4<0 i 4+3а<0, розв’язки системи: ає(-oo; -4/3)
Таким чином, маємо таку множину параметрів: aбо a<-4/3 або a>-2/3
Відповідь: Якщо параметр a<-4/3 або a>-2/3, то рівняння
-3ах + 4а = -2а+4х-4
з невідомим х має тільки додатний корінь х = (6а+4)/4+3а).
Реалізація мовою програмування Python3.
print('Якщо параметр a<-4/3 або a>-2/3, то рівняння -3ах + 4а = -2а+4х-4 ')
print(' має додатний корінь х = (6а+4)/(4+3а) ')
print(' Корені рівняння для цього випадку:')
k=300; a1=-4/3; a2=-2/3; h=10/k; a=['None']*k; b=['None']*k;
for j in range(3,k):
a[j]=float(a1-float(h*j)); b[j]=float(a2+float(h*j));
za=float((6*a[j]+4)); zb=float((6*b[j]+4));
ua=float(4+3*a[j]); ub=float(4+3*b[j]);
xa=float(za/ua); xb=float(zb/ub);
print(j,'-ий випадок. Якщо параметр a1=',a[j],' то корінь рівняння x(a1)=',xa)
print(j,'-ий випадок. Якщо параметр a2=',b[j],' то корінь рівняння x(a2)=',xb)
Протестувати програму декілька разів.
Тест 1. Якщо k=13.
Тест 2. Якщо k=19.
Тест 3. Якщо k=20.
Запитання 3. Як аналізувати математичні моделі лінійних рівнянь з параметрами, якщо корені рівняння мають бути тільки протилежними числами?
Відповідь. Продемонструємо зразок аналізу такого лінійного рівняння з параметром.
Завдання 3.Знайти усі значення параметра а, при яких рівняння |аx-3a|=5+2а
з невідомим х має лише протилежні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Аналіз математичної моделі.
|аx-3a|=5+2а
аx-3a=5+2а; аx-3a=-5-2а;
а(x-3)=5+2а; а(x-3)=-5-2а;
а)якщо а=0, то рівняння немає розв’язків. Тому, що
0*(х-3)=5; 0*(х-3)=-5
б)якщо а< >0, то рівняння має розв’язки.
x1=5/а+5; x2=-5/а+1;
Відповідно умові завдання, отримаємо рівняння для двох протилежних коренів:
5/а+5=-(-5/а+1)
5/а-5/а = 4;
0<>4
Таким чином, не існує таких параметрів а, при якому дане рівняння мало би два корені у вигляді протилежних чисел.
Реалізація мовою програмування Python3.
print('Якщо параметр a-дійсне число, то рівняння |аx-3a|=5+2а')
print('при a<>0 має два корені x1=5/а+5; x2=-5/а+1; ')
print(' Корені цього рівняння не можуть бути протилежними числами:')
k=5; a1=-0.5; a2=0.5; h=10/k; a=['None']*k; b=['None']*k;
for j in range(3,k,2):
a[j]=float(a1-float(h*j)); b[j]=float(a2+float(h*j));
x1=float((5/a[j]+5)); x2=float((-5/a[j]+1));
print(j,'-ий випадок. Якщо параметр a1=',a[j],' то корінь рівняння x1(a1)=',x1, 'x2(a1)=',x2)
if x1==-x2:
print('Рівняння має протилежні корені: x1(a1)=',x1, 'x2(a1)=',x2)
else:
print('Рівняння немає протилежні корені')
x3=float((5/b[j]+5)); x4=float((-5/b[j]+1));
print(j+1,'-ий випадок. Якщо параметр a2=',b[j],' то корінь рівняння x3(a2)=',x3, 'x4(a2)=',x4)
if x3==-x4:
print('Рівняння має протилежні корені: x3(a1)=',x3, 'x4(a1)=',x4)
else:
print('Рівняння немає протилежні корені')
Протестувати програму декілька разів.
Тест 1. Якщо k=40.
Тест 2. Якщо k=10.
Тест 3. Якщо k=90.
Запитання 4. Як аналізувати математичні моделі лінійних рівнянь з параметрами, якщо корені рівняння мають бути тільки непарними числами?
Відповідь. Продемонструємо зразок аналізу такого лінійного рівняння з параметром.
Завдання 4. Знайти усі значення параметра а, при яких рівняння
-4ах + 5а = -6а+3х-2
з невідомим х має тільки непарні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Аналіз математичної моделі.
-4ах + 5а = -6а+3х-2
-4ах-3x = -6а-5a-2
-(4а+3)x = -(11а+2)
(4а+3)x = (11а+2)
Якщо а =-0.75 то рівняння немає коренів.
Якщо а <>-0.75 то рівняння має корінь.
x = (11а+2)/(4а+3)
Відповідно умові завдання, отримаємо рівняння для непарних чисел:
2m-1= (11а+2)/(4а+3) , де m - ціле число
Звідси,
А=(6m-5)/( 15-8m), де m - ціле число
Таким чином, при таких параметрів а=(6m-5)/( 15-8m),
де m - ціле число дане рівняння -4ах + 5а = -6а+3х-2
має непарний корінь у вигляді 2m-1=(11а+2)/(4а+3) .
Реалізація мовою програмування Python3.
print('Якщо параметри а=(6m-5)/(15-8m), де m - ціле число, дане рівняння: -4ах + 5а = -6а+3х-2 ')
print('має непарний корінь у вигляді х=2m-1=(11а+2)/(4а+3) ')
print('Корені цього рівняння можуть бути непарними числами:')
k=10; a1=-0.5; a2=0.5; h=10/k; a=['None']*k;
for j in range(0,k,1):
a[j]=float(6*j-5)/float(15-8*j);
x1=float(11*a[j]+2)/float((4*a[j]+3));
print(j,'-ий випадок. Якщо параметр a1=',a[j],' то корінь рівняння x1(a1)=',round(x1,0))
Протестувати програму декілька разів.
Тест 1. Якщо k=14.
Тест 2. Якщо k=20.
Тест 3. Якщо k=50.
Запитання 5. Як аналізувати математичні моделі лінійних рівнянь з параметрами, якщо корені рівняння мають бути тільки парними числами?
Відповідь. Продемонструємо зразок аналізу такого лінійного рівняння з параметром.
Завдання 5. Знайти усі значення параметра а, при яких рівняння
-5ах + а = -2а+х-1
з невідомим х має тільки парні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Аналіз математичної моделі.
-5ах + а = -2а+х-1
-5ах -x = -2а-a-1
-(5a-1)x =-(3a+1)
Якщо а =0.2 то рівняння немає коренів.
Якщо а <>0.2 то рівняння має корінь.
x=(3a+1)/(5a-1)
Відповідно умові завдання, отримаємо рівняння для парних чисел:
2m=(3a+1)/(5a-1), де m - ціле число
Звідси,
a=(2m+1)/(10m-3), де m - ціле число
Таким чином, при таких параметрів а=(2m+1)/(10m-3),
де m - ціле число дане рівняння -5ах + а = -2а+х-1
має парний корінь у вигляді 2m=(3a+1)/(5a-1).
Реалізація мовою програмування Python3.
print('Якщо параметри а=(2m+1)/(10m-3),де m - ціле число дане рівняння -5ах + а = -2а+х-1 ')
print('має парний корінь у вигляді 2m=(3a+1)/(5a-1). ')
print('Корені цього рівняння можуть бути парними числами:')
k=10; a1=-0.5; a2=0.5; h=10/k; a=['None']*k;
for j in range(0,k,1):
a[j]=float(2*j+1)/float(10*j-3);
x1=float(3*a[j]+1)/float((5*a[j]-1));
print(j,'-ий випадок. Якщо параметр a1=',a[j],' то корінь рівняння x1(a1)=',round(x1,0))
Протестувати програму декілька разів.
Тест 1. Якщо k=20.
Тест 2. Якщо k=15.
Тест 3. Якщо k=70.
Практична частина
Алгоритми мовою Python для знаходження розв’язків рівнянь кубічного виду
з двома змінними в цілих числах.
Завдання 1. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними: x3+x2y+xy2+y3=0.
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
x3+x2y+xy2+y3=0.
Розкладемо на множиники способом групування:
(x^2-y^2)(y+x)=0
Отже маємо такі розв’язки:
x1=-y1
x2=y2
Тобто цілі розв’язки рівняння - це пара двійок цілих чисел:
(x1; y1) = (k; -k), де k - цілі числа
(x2; y2) =(m; m), де m - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння x^3+x^2y+xy^2+y^3=0')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for m in range(1,t):
l=l+1
v[i]=k #x1
f[i]=-k #y1
w[i]=m #x2
h[i]=m #y2
# w3[i]=2+5*n #x3
#h3[i]=3+4*n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння 8x^2+2xy-15y^2+50x-24y+63=0, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння 8x^2+2xy-15y^2+50x-24y+63=0, (x2,y2)=(',w[i],'; ',h[i],')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=5;
Тест2. Якщо t=7; p=6;
Тест3. Якщо t=6; p=10
Завдання 2. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними:
54x3+72x2y-24xy2-32y3=0.
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
54x3+72x2y-24xy2-32y3=0.
Розкладемо на множиники способом групування:
2(3x-2y)(3x+2y)(3x+4y)=0
(9x^2-4y^2)(8y+6x)=0
Отже маємо такі розв’язки:
x1=2k, y1=3k, де k - цілі числа
x2=-2m, y2=3m, де m - цілі числа
x3=4n, y3=-3n, де n - цілі числа
Тобто цілі розв’язки рівняння - це три пари цілих чисел:
(x1; y1) = (2k; 3k), де k - цілі числа
(x2; y2) =(-2m; 3m), де m - цілі числа
(x3; y3) =(4n; -3n), де n - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння 54x^3+72x^2y-24xy^2-32y^3=0')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for n in range(1,t):
l=l+1
v[i]=2*k #x1
f[i]=3*k #y1
w[i]=-2*m #x2
h[i]=3*m #y2
w3[i]=4*n #x3
h3[i]=-3*n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння 54x^3+72x^2y-24xy^2-32y^3=0, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння 54x^3+72x^2y-24xy^2-32y^3=0, (x2,y2)=(',w[i],'; ',h[i],')')
print(l,' -a 3-двійка чисел, що є розвязком рівняння 54x^3+72x^2y-24xy^2-32y^3=0, (x3,y3)=(', w3[i],'; ',h3[i], ')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=5;
Тест2. Якщо t=6; p=7;
Тест3. Якщо t=8; p=9
Завдання 3. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними:
15x3+154x2y-135xy2-154y3=0
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
15x3+154x2y-135xy2-154y3=0
Розкладемо на множиники способом групування:
(5x-7y)(3x+2y)(x+11y)=0
Отже маємо такі розв’язки:
x1=7k, y1=5k, де k - цілі числа
x2=-2m, y2=3m, де m - цілі числа
x3=11n, y3=-n, де n - цілі числа
Тобто цілі розв’язки рівняння - це три пари цілих чисел:
(x1; y1) = (7k; 5k), де k - цілі числа
(x2; y2) =(-2m; 3m), де m - цілі числа
(x3; y3) =(11n; -n), де n - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння 15x^3+154x^2y-135xy^2-154y^3=0')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for n in range(1,t):
l=l+1
v[i]=7*k #x1
f[i]=5*k #y1
w[i]=-2*m #x2
h[i]=3*m #y2
w3[i]=11*n #x3
h3[i]=-n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння 15x^3+154x^2y-135xy^2-154y^3=0, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння 15x^3+154x^2y-135xy^2-154y^3=0, (x2,y2)=(',w[i],'; ',h[i],')')
print(l,' -a 3-двійка чисел, що є розвязком рівняння 15x^3+154x^2y-135xy^2-154y^3=0, (x3,y3)=(', w3[i],'; ',h3[i], ')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=5;
Тест2. Якщо t=8; p=8;
Тест3. Якщо t=6; p=10
Завдання 4. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними:
-360x3+246x2+162x-108 -56y3+174y2+18y+478x2y-82xy2-408xy=0
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
-360x3+246x2+162x-108 -56y3+174y2+18y+478x2y-82xy2-408xy=0
Розкладемо на множиники способом групування:
(9x-7y+6)(-5x+4y+3)(8x+2y-6)=0
Отже маємо такі розв’язки:
x1=3+4k, y1=3+5k, де k - цілі числа
x2=7m+4, y2=9m+6, де m - цілі числа
x3=n, y3=3-4n, де n - цілі числа
Тобто цілі розв’язки рівняння - це три пари цілих чисел:
(x1; y1) = (3+4k; 3+5k), де k - цілі числа
(x2; y2) =(7m+4; 9m+6), де m - цілі числа
(x3; y3) =(n; 3-4n), де n - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння -360x^3+246x^2+162x-108-56y^3+174y^2+18y+478x^2y-82xy^2-408xy=0')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for n in range(1,t):
l=l+1
v[i]=3+4*k #x1
f[i]=3+5*k #y1
w[i]=4+7*m #x2
h[i]=6+9*m #y2
w3[i]=n #x3
h3[i]=3-4*n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння, (x2,y2)=(',w[i],'; ',h[i],')')
print(l,' -a 3-двійка чисел, що є розвязком рівняння, (x3,y3)=(', w3[i],'; ',h3[i], ')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=5;
Тест2. Якщо t=7; p=8;
Тест3. Якщо t=6; p=9
Завдання 5. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними:
-189x3+222x2-27x-6 -96y3+124y2+34y+204x2y+76xy2-338xy=0
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
-189x3+222x2-27x-6 -96y3+124y2+34y+204x2y+76xy2-338xy=0
Розкладемо на множиники способом групування:
(9x-8y+1)(-7x+6y+2)(3x+2y-3)=0
Отже маємо такі розв’язки:
x1=1+2k, y1=-3k, де k - цілі числа
x2=6m+2, y2=7m+2, де m - цілі числа
x3=7+8n, y3=8+9n, де n - цілі числа
Тобто цілі розв’язки рівняння - це три пари цілих чисел:
(x1; y1) = (1+2k; -3k), де k - цілі числа
(x2; y2) =(6m+2; 7m+2), де m - цілі числа
(x3; y3) =(7+8n; 8+9n), де n - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння -189x^3+222x^2-27x-6-96y^3+124y^2+34y+204x^2y+76xy^2-338xy=0')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for n in range(1,t):
l=l+1
v[i]=1+2*k #x1
f[i]=-3*k #y1
w[i]=2+6*m #x2
h[i]=2+7*m #y2
w3[i]=7+8*n #x3
h3[i]=8+9*n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння, (x2,y2)=(',w[i],'; ',h[i],')')
print(l,' -a 3-двійка чисел, що є розвязком рівняння, (x3,y3)=(', w3[i],'; ',h3[i], ')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=6;
Тест2. Якщо t=7; p=7;
Тест3. Якщо t=6; p=8
Завдання 6. Створити та реалізувати мовою програмування Python в середовищі програмування Thonny алгоритм для знаходження двійок цілих чисел, що задовольняють нелінійне рівняння з двома змінними:
x3+3x2+3x+1+y3-y2-y-x2y-xy2-2xy=0.
Моделювання алгоритму.
Проаналізуємо математичну модель даного рівняння для створення алгоритму.
Знайдемо аналітично розв’язки даного рівняння в цілих числах
x3+3x2+3x+1+y3-y2-y-x2y-xy2-2xy=0.
Розкладемо на множиники способом групування:
(x-y+1)(-x+y-1)(-x-y-1)=0
Отже маємо такі розв’язки:
x1=k, y1=-k-1, де k - цілі числа
x2=m, y2=m+1, де m - цілі числа
x3=-n, y3=-n+1, де n - цілі числа
Тобто цілі розв’язки рівняння - це три пари цілих чисел:
(x1; y1) = (k; -k-1), де k - цілі числа
(x2; y2) =(m; m+1), де m - цілі числа
(x3; y3) =(-n; -n+1), де n - цілі числа
Реалізація алгоритму.
print('Алгоритм пошуку цілих pозвязків нелінійного рівняння x^3+3x^2+3x+1+y^3-y^2-y-x^2y-xy^2-2xy=0.')
p=4; t=3;
w=['None']*p; v=['None']*p; f=['None']*p;
h=['None']*p; h3=['None']*p; w3=['None']*p;
l=0
for i in range(p):
for k in range(1,t):
for m in range(1,t):
for n in range(1,t):
l=l+1
v[i]=k #x1
f[i]=-1-k #y1
w[i]=m #x2
h[i]=1+m #y2
w3[i]=-n #x3
h3[i]=1-n #y3
print(l,' -a 1-двійка чисел, що є розвязком рівняння, (x1,y1)=(', v[i],'; ',f[i], ')')
print(l,' -a 2-двійка чисел, що є розвязком рівняння, (x2,y2)=(',w[i],'; ',h[i],')')
print(l,' -a 3-двійка чисел, що є розвязком рівняння, (x3,y3)=(', w3[i],'; ',h3[i], ')')
Протестувати програму декілька разів:
Тест1. Якщо t=5; p=10;
Тест2. Якщо t=7; p=12;
Тест3. Якщо t=6; p=15
Результат виконаної практичної роботи це файли( із результатами тестування програм) надіслати вашому учителю на електронну скриньку:
vinnser@gmail.com (Сергій Петрович)
ktdfz@i.ua (Юрій Васильович)
*********************
*****************
Додаткові завдання для самостійного вироблення умінь, навичок компетенцій учнів
Для наступних завдань записати, реалізувати програму мовою програмування та протестувати її на правильність.
Завдання на програмування мовою Pascal або Python
Початковий рівень
Завдання з програмування слідувань
Для наступних завдань записати, реалізувати програму мовою програмування та протестувати її на правильність.
Завдання 1.0 Дано відстань L в сантиметрах. Використовуючи операцію ділення без остачі, знайти кількість повних метрів в нім (1 метр = 100 см).
Завдання 1.1. Дано тризначне число. Вивести спочатку його останню цифру (одиниці), а потім - його середню цифру (десятки).
Завдання 1.2. З початку доби пройшло N секунд (N - ціле). Знайти кількість повних годин, що пройшло з початку доби.
Завдання 2.0 Дано маса M в кілограмах. Використовуючи операцію ділення без остачі знайти кількість повних тонн в ній (1 тонна = 1000 кг).
Завдання 2.1. Дано тризначне число. Знайти суму і добуток його цифр.
Завдання 2.2. З початку доби пройшло N секунд (N - ціле). Знайти кількість секунд, що пройшли з початку останньої хвилини.
Завдання 3.0 Даний розмір файлу в байтах. Використовуючи операцію ділення без остачі знайти кількість повних кілобайт, які займає даний файл (1 кілобайт = 1024 байти).
Завдання 3.1. Дано тризначне число. У нім закреслили першу зліва цифру приписали її справа. Вивести отримане число.
Завдання 3.2. З початку доби пройшло N секунд (N - ціле). Знайти кількість секунд, що пройшли з початку останньої години.
Завдання 4.0 Дані цілі позитивні числа A і B (A > B). На відрізку довжини A розміщена максимально можлива кількість відрізків довжини В (без накладень). Використовуючи операцію ділення без остачі, знайти кількість відрізків B, розміщених на відрізку A.
Завдання 4.1. Дано тризначне число. Вивести число, отримане при прочитанні початкового числа справа наліво.
Завдання 4.2. З початку доби пройшло N секунд (N - ціле). Знайти кількість повних хвилин, що пройшли з початку останньої години.
Завдання 5.0 Дані цілі позитивні числа A і B (A > B). На відрізку довжини розміщена максимально можлива кількість відрізків довжини B (без накладень). Використовуючи операцію узяття залишку від ділення без остачі, найти довжину незайнятої частини відрізку A.
Завдання 5.1. Дано тризначне число. У нім закреслили першу справа цифру і приписали її зліва. Вивести отримане число.
Завдання 5.2. Дні тижня пронумеровані таким чином: 0 – нeділя, 1 - понеділок, 2 - вівторок . . ., 6 - субота. Дано ціле число K, що в діапазоні 1-365. Визначити номер дня тижня для K -го дня року, якщо відомо, що цього року 1 січня було понеділком.
Середній рівень
Складіть програми мовою програмування
або Scratch або Python або Pascal
для розв´язування наступних задач
Завдання з програмування слідувань
D1.Програма задає два випадкових додатних парних числа k та b. Створити алгоритм мовою програмування, який спочатку додає до кожного числа однакове випадкове число, що більше 102, а потім знаходить потроєну суму двох чисел. А в остаточному результаті виводить остачу від ділення знайденої суми на 12.
D2. Програма задає два випадкових непарних числа k та b, що більші, ніж 199 і менші 899. Створити алгоритм мовою програмування, який спочатку знаходить квадрати обох чисел, а потім середнє арифметичне цих квадратів. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 13.
D3. Програма задає два випадкових непарних числа k та b, що більші, ніж 399 і менші 999. Створити алгоритм мовою програмування, який спочатку знаходить більше число та його квадрат , а потім знаходить куб меншого числа, а потім знаходить їхнє середнє арифметичне квадрату та кубу. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 19.
D4. Програма задає два випадкових непарних числа k та b, що більші, ніж 499 і менші 799. Створити алгоритм мовою програмування, який спочатку знаходить більше число та його подвоює, а потім знаходить потроєне менше число, а потім знаходить їхнє середнє арифметичне. А в остаточному результаті виводить остачу від ділення середнього арифметичного на 17.
**************************
Завдання E
Завдання з програмування слідувань та розгалужень
E1. Дано два випадкових числа. Визначити більше з двох чисел за допомогою таких трьох дій.
1. Знайти середнє арифметичне двох чисел.
2. Знайти модуль різниці двох чисел.
3. Додати два попередні результати.
Упорядкувати ці числа за зростання.
E2. Дано два випадкових числа. Визначити менше з двох чисел за допомогою таких дій.
1)Знайти середнє арифметичне двох чисел.
2)Знайти модуль різниці двох чисел.
3)Від середнього арифметичного відняти модуль різниці, тобто, відняти два попередні результати.
Упорядкувати ці числа за спаданням.
E3. Дано три випадкових числа. Визначити більше з таких трьох чисел за допомогою умовних операторів розгалуження. Упорядкувати ці числа за спаданням.
E4. Дано три випадкових числа. Визначити менше з таких трьох чисел за допомогою умовних операторів розгалуження. Упорядкувати ці числа за зростання.
E5. Дано чотири випадкових числа. Визначити більше з таких чисел за допомогою умовних операторів розгалуження. Упорядкувати ці числа за спаданням.
E6 Дано чотири випадкових числа. Визначити менше з таких чисел за допомогою умовних операторів розгалуження. Упорядкувати ці числа за зростанням.
Достатний рівень
Додаткові завдання для самостійного вироблення умінь, навичок компетенцій учнів
Для наступних завдань записати, реалізувати програму мовою програмування та протестувати її на правильність.
Програмування з одновимірними масивами
Завдання А. Одновимірні масиви
А1. Задано одновимірний масив на 10 елементів типу випадкових цілих чисел із числового проміжку (-100;100). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на протилежні за знаком.
А2. Задано одновимірний масив на 5 елементів типу випадкових цілих чисел із числового інтервалу (-150; 120). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на квадрати.
А3. Задано одновимірний масив на 7 елементів типу випадкових цілих чисел із числового інтервалу (-950; 820). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на вдвічі збільшені.
А4. Задано одновимірний масив на 8 елементів типу випадкових дробових чисел із числового інтервалу (-9; 8). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість додатних елементів масиву.
А5. Задано одновимірний масив на 20 елементів типу випадкових дробових чисел із числового інтервалу (-95; 80). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість від´ємних елементів масиву.
А6. Задано одновимірний масив на 18 елементів типу випадкових дробових чисел із числового інтервалу (-29; 89). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість додатних елементів масиву.
А7. Задано одновимірний масив на 20 елементів типу випадкових дробових чисел із числового інтервалу (-95; 80). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість від´ємних елементів масиву.
А8. Задано одновимірний масив на 12 елементів типу випадкових дробових чисел із числового інтервалу (-79; 89). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне додатних елементів масиву.
А9. Задано одновимірний масив на 10 елементів типу випадкових дробових чисел із числового інтервалу (-65; 60). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне від´ємних елементів масиву.
А10. Задано одновимірний масив на 10 елементів типу випадкових дробових чисел із числового інтервалу (-65; 60). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість парних від´ємних елементів масиву.
Завдання В. Одновимірні масиви
В1. Задано одновимірний масив на 17 елементів типу випадкових дробових чисел із числового інтервалу (-95; 100). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне найбільшого та найменшого від´ємних елементів масиву.
В2. Задано одновимірний масив на 18 елементів типу випадкових дробових чисел із числового інтервалу (-25; 30). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне найбільшого та найменшого додатних елементів масиву.
В3. Задано одновимірний масив на 19 елементів типу випадкових дробових чисел із числового інтервалу (-95; 90). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує квадрат різниці найбільшого та найменшого додатних елементів масиву.
В4. Задано одновимірний масив на 14 елементів типу випадкових дробових чисел із числового інтервалу (-95; 70). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує куб різниці найбільшого та найменшого від´ємних елементів масиву.
В5. Задано одновимірний масив на 22 елементи типу випадкових дробових чисел із числового інтервалу (-85; 90). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів додатних елементів масиву.
В6. Задано одновимірний масив на 15 елементів типу випадкових дробових чисел із числового інтервалу (-95; 70). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму кубів від´ємних елементів масиву.
В7. Задано одновимірний масив на 6 елементів типу випадкових дробових чисел із числового інтервалу (-95; -9). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів для трьох найбільших елементів масиву.
В8. Задано одновимірний масив на 5 елементів типу випадкових дробових чисел із числового інтервалу (-195; 0). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму кубів чотирьох найменших елементів масиву.
В9. Задано одновимірний масив на 11 елементів типу випадкових цілих чисел із числового інтервалу (-135; 120). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів трьох парних найменших елементів масиву.
В10. Задано одновимірний масив на 13 елементів типу випадкових цілих чисел із числового інтервалу (-415; 620). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів трьох непарних найбільших елементів масиву.
Завдання С. Одновимірні масиви
С1. Задано одновимірний масив на 19 елементів типу випадкових цілих чисел із числового інтервалу (-295; 300). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює парні елементи(числа) на найбільший елемент масиву та непарні елементи(числа) масиву замінює на найменший елемент масиву.
С2. Задано одновимірний масив на 17 елементів типу випадкових цілих чисел із числового інтервалу (-285; 280). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи(числа) , що більші 5 і менші 100 на найбільший елемент масиву та елементи(числа) масиву , що більші -100 і менші 10, замінює на найменший елемент масиву.
С3. Задано одновимірний масив на 18 елементів типу випадкових цілих чисел із числового інтервалу (-485; 380). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму додатних елементів масиву, що мають парні індекси.
С4. Задано одновимірний масив на 16 елементів типу випадкових цілих чисел із числового інтервалу (-575; 580). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають непарні індекси.
С5. Задано одновимірний масив на 31 елементів типу випадкових цілих чисел із числового інтервалу (-485; 380). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму додатних елементів масиву, що мають індекси, які при діленні на 3 дають остачу 2.
С6. Задано одновимірний масив на 24 елементів типу випадкових цілих чисел із числового інтервалу (-695; 680). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають індекси, які при діленні на 5 дають остачу 3.
С7. Задано одновимірний масив на 41 елементів типу випадкових цілих чисел із числового інтервалу (-985; 980). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму квадратів додатних елементів масиву, що мають індекси, які при діленні на 4 дають остачу 2.
С8. Задано одновимірний масив на 34 елементів типу випадкових цілих чисел із числового інтервалу (-275; 180). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають індекси, які при діленні на 7 дають остачу 6.
С9. Задано одновимірний масив на 50 елементів типу випадкових цілих чисел із числового інтервалу (-1085; 980). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму квадратів додатних елементів масиву, що мають індекси, які при діленні на 12 дають остачу 2.
С10. Задано одновимірний масив на 64 елементів типу випадкових цілих чисел із числового інтервалу (-1275; 1180). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму кубів від´ємних елементів масиву, що мають індекси, які при діленні на 9 дають остачу 8.
Високий рівень
Завдання на програмування мовою Pascal або Python
Двовимірні масиви
Завдання А1. Двовимірні масиви(матриці)
А1. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових цілих чисел із числового проміжку (-100;100). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на протилежні за знаком.
А2. Задано двовимірний масив розміром 5х4( 5 рядків, чотири стовпці) елементів типу випадкових цілих чисел із числового інтервалу (-150; 120). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на квадрати.
А3. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових цілих чисел із числового інтервалу (-950; 820). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи в заданому масиві на вдвічі збільшені.
А4. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-9; 8). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість додатних елементів масиву.
А5. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-95; 80). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість від´ємних елементів масиву.
А6. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-29; 89). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість додатних елементів масиву.
А7. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-95; 80). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість від´ємних елементів масиву.
А8. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-79; 89). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне додатних елементів масиву.
А9. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-65; 60). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне від´ємних елементів масиву.
А10. Задано двовимірний масив розміром 3х4(три рядки, чотири стовпці) елементів типу випадкових дробових чисел із числового інтервалу (-65; 60). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує кількість парних від´ємних елементів масиву.
Завдання В1. Двовимірні масиви(матриці)
В1. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-95; 100). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне найбільшого та найменшого від´ємних елементів масиву.
В2. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-25; 30). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує середнє арифметичне найбільшого та найменшого додатних елементів масиву.
В3. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів випадкових дробових чисел із числового інтервалу (-95; 90). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує квадрат різниці найбільшого та найменшого додатних елементів масиву.
В4. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-95; 70). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує куб різниці найбільшого та найменшого від´ємних елементів масиву.
В5. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-85; 90). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів додатних елементів масиву.
В6. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-95; 70). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму кубів від´ємних елементів масиву.
В7. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-95; -9). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів для трьох найбільших елементів масиву.
В8. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових дробових чисел із числового інтервалу (-195; 0). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму кубів чотирьох найменших елементів масиву.
В9. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-135; 120). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів трьох парних найменших елементів масиву.
В10. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-415; 620). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який підраховує суму квадратів трьох непарних найбільших елементів масиву.
Завдання С1. Двовимірні масиви(матриці)
С1. Задано двовимірний масив розміром 5х5(5 рядків, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-295; 300). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює парні елементи(числа) на найбільший елемент масиву та непарні елементи(числа) масиву замінює на найменший елемент масиву.
С2. Задано двовимірний масив розміром 5х5(5 рядків, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-285; 280). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який замінює елементи(числа) , що більші 5 і менші 100 на найбільший елемент масиву та елементи(числа) масиву , що більші -100 і менші 10, замінює на найменший елемент масиву.
С3. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-485; 380). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму додатних елементів масиву, що мають парні праві або ліві індекси.
С4. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-575; 580). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають непарні праві або ліві індекси.
С5. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-485; 380). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму додатних елементів масиву, що мають праві та ліві індекси, які при діленні на 3 дають остачу 1.
С6. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-695; 680). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають праві та ліві індекси, які при діленні на 5 дають остачу 1.
С7. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-985; 980). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму квадратів додатних елементів масиву, що мають праві та ліві індекси, які при діленні на 4 дають остачу 2.
С8. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-275; 180). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму від´ємних елементів масиву, що мають праві та ліві індекси, які при діленні на 7 дають остачу 4.
С9. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-1085; 980). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму квадратів додатних елементів масиву, що мають праві та ліві індекси, які при діленні на 12 дають остачу 2.
С10. Задано двовимірний масив розміром 4х5(4 рядки, 5 стовпців) елементів типу випадкових цілих чисел із числового інтервалу (-1275; 1180). Створити алгоритм мовою програмування Python в середовищі програмування Thonny, який знаходить суму кубів від´ємних елементів масиву, що мають праві та ліві індекси, які при діленні на 9 дають остачу 3.
Завдання для колективного опрацювання в маленьких групах.
Завдання 1. Знайти такі значеннях параметра а, при яких рівняння
-4х + 2а +8= -5а+4ах-10
з невідомим х має тільки від’ємні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 2. Знайти усі такі значеннях параметра а, при яких рівняння
-5ах + 2а = -10а+4х-1
з невідомим х має тільки додатні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 3.Знайти усі значення параметра а, при яких рівняння
а|x|=(2+4а)
з невідомим х має лише протилежні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 4. Знайти усі значення параметра а, при яких рівняння
-4ах +2а = -6а+5х-4
з невідомим х має тільки непарні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 5. Знайти усі значення параметра а, при яких рівняння
-4ах + 2а = -5а+2х+10
з невідомим х має тільки парні корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 6. Вказати усі такі значення параметра а, при яких рівняння
-5ах + 8а=4а-5
з невідомим х має тільки цілі корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 7. Вказати усі такі значення параметра а, при яких рівняння
-4ах + 4а=4а-4х+2
з невідомим х має тільки цілі корені. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 8. Вказати усі такі значення параметра а, при яких рівняння
(2-4а)(6-3а)х =(4а-8)(-2а+1)
з невідомим х має безліч коренів. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 9. Вказати усі такі значення параметра а, при яких рівняння
-5ах + 2х+10 = 8-4а;
з невідомим х має тільки один корінь вигляду 4n+2, де n- ціле число. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 10. Вказати усі такі значення параметра а, при яких рівняння
(8+4|а|)(50-2|а|)х =(а+5)(-6|а|+6)
з невідомим х не має коренів. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 11. Знайти усі такі значення параметра а, при яких розв’язок рівнянь
-6а+50-8|х| = -4а+40
знаходиться на проміжку -4 <х< 6. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання 12. Знайти усі такі значення параметра а, при яких розв’язок рівнянь
2-4|х|-а = а-1
знаходиться на проміжку 3 <|х| < 9. Створити та реалізувати алгоритми мовою програмування Python3 для пошуку унікальних коренів лінійних рівнянь з параметром відповідно вказаним властивостям коренів рівняння.
Завдання на розвиток кмітливості




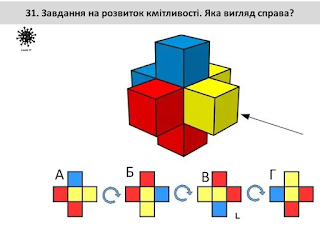






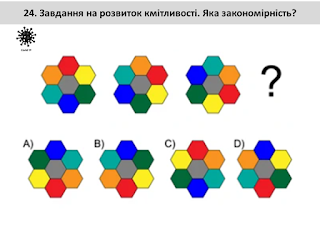









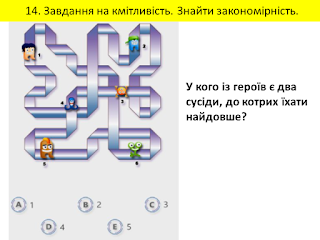

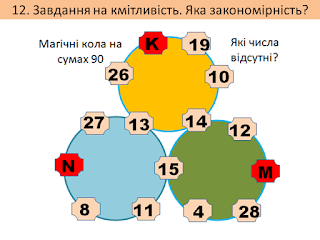










Немає коментарів:
Дописати коментар