Задача Вінницького про потужність комунікацій

Задача Вінницького

про  потужність комунікацій в соціальній мережі

Умова задачі: 

Один власник акаyнту в соціальній мережі розсилає  n різних повідомлень 1-го рівня  для n  одержувачів(кожний одержувач отримує тільки одне повідомлення 1-го рівня). Згодом кожний одержувач повідомлення  1-го рівня розсилає n-1 повідомлень 2-го рівня для n-1  одержувачів(при цьому кожний одержувач отримує тільки одне повідомлення 2-го рівня і   не отримував повідомлення  1-го рівня).  Після цього, кожний одержувач повідомлення  2-го рівня розсилає n-2 повідомлень 3-го рівня для n-2  одержувачів(при цьому кожний одержувач отримує тільки одне повідомлення 3-го рівня і не отримував повідомлень 1-го та 2-го рівнів).    І так далі.   Таким чином, кожний одержувач повідомлень  m-го рівня розсилає повідомлення  n-m  повідомлень   (m+1)-го рівня для   n-m  одержувачів(при цьому кожний одержувач отримує тільки одне повідомлення (m+1)-го  рівня і   не отримував повідомлень  менших за номером m+1 рівнів).   Зрозуміло, якщо n=m, то  розсилання  повідомлень  припиняється(тобто, це означає, що  повідомлень (n+1 )-го рівня не розсилалося вже нікому).  Допоможіть  адміністратору соціальної мережі  автоматично розраховувати  таку суму, яка містить два доданки: 1) кількість  усіх осіб, котрі задіяні у цій комунікації; 2)кількість усіх повідомлень будь-якого рівня у цій комунікації.

Технічні умови для програмування. Програма  Measure читає з пристрою стандартного введення натуральне число n, не менші за 1 та не більші  50. Число n – це кількість різних повідомлень 1-го  для n  одержувачів.   Програма виводить на пристрій стандартного виведення єдине число — суму, яка має два доданки: 1) кількість  усіх осіб, котрі задіяні у цій мережній комунікації; 2)кількість усіх повідомлень будь-якого рівня у цій мережній комунікації.

Приклади

Введення	Виведення
3	31
5	651

Розв’язування.  Створимо математичну модель до цієї задачі. Згідно умови задачі створюємо простий граф(дерево), в якому будь-яка вершина позначає особу, а будь-яке ребро означає повідомлення певного рівня(кольору)) для n=3;

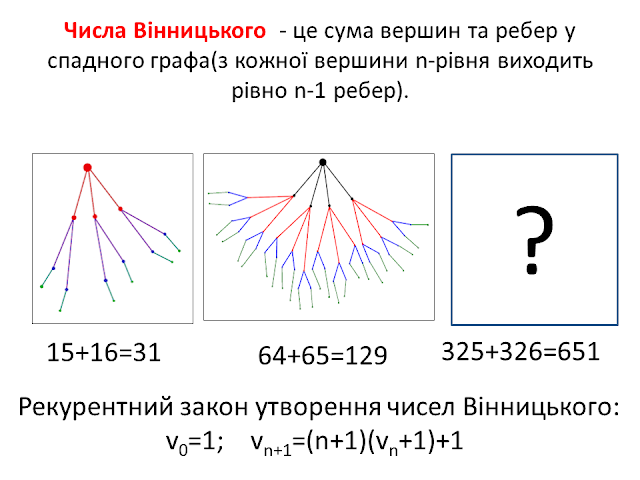
Згідно умови задачі створюємо простий граф для n=3;

Розрахунки: Кількість повідомлень: 15. Кількість осіб 16. Сума: 31.

Згідно умови задачі створюємо простий граф для n=4;

Розрахунки: Кількість повідомлень: 64. Кількість осіб 65. Сума: 129.

Простий граф(для n=4) містить в собі чотири підграфи(випадку n=3), тому використаємо математичну індукцію для виведення рекурентної формули.

Проаналізуємо  перехід від індуктивного кроку n=k   до наступного кроку n=k+1 і 

 отримаємо рекурентний закон 

розрахунку  потрібної для адміністратора суми для довільного k:

v₀=1;    v_k=k(v_k-1+1)+1 ,   якщо k – натуральне число.

V₁=3;     

V₂=9;   

V₃=31;  

V₄=129;  

V₅=651;    

V₆=3913;

V₇=27399;     
V₈=219201;     
V₉=1978819;        
V₁₀=19728201, і так далі.

Якщо мережа побудована за зростаючою властивістю простого графа, то отримаємо числа Павліяна